Scan-Converting a circle using Bresenham's algorithm works as follows: Points are generated from 90° to 45°, moves will be made only in the +x & -y directions as shown in fig:
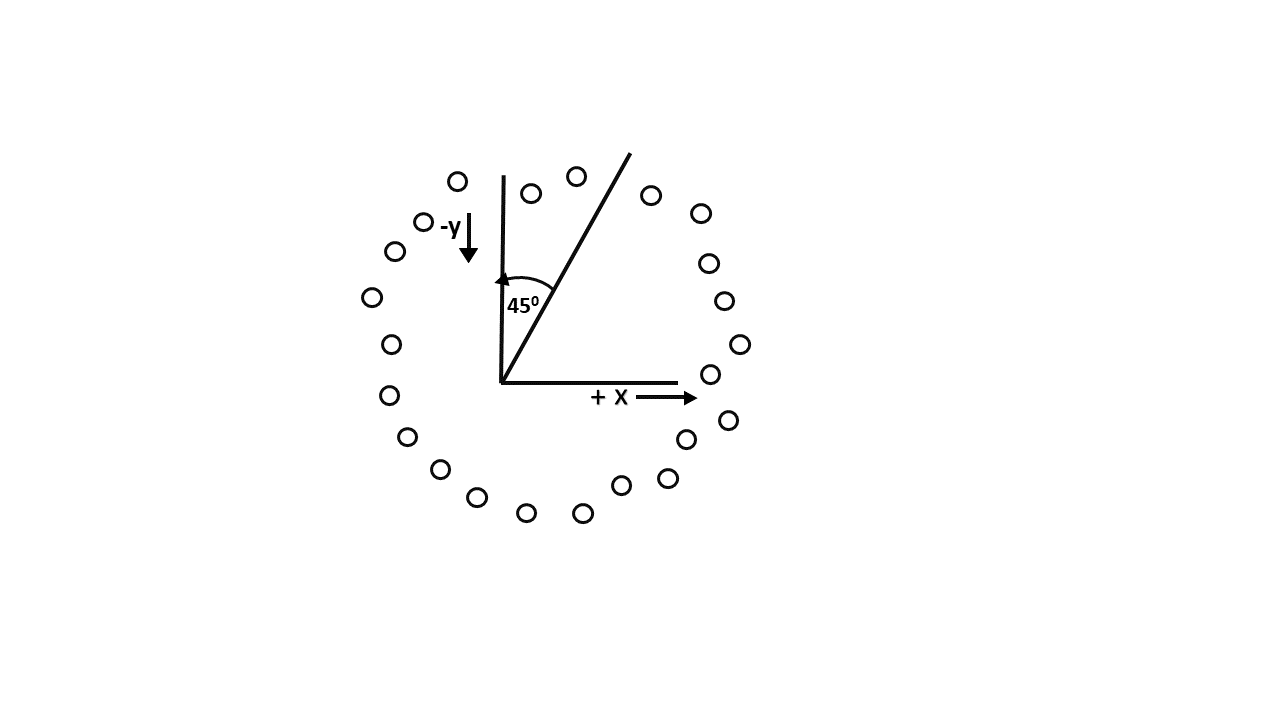
The best approximation of the true circle will be described by those pixels in the raster that falls the least distance from the true circle. We want to generate the points from
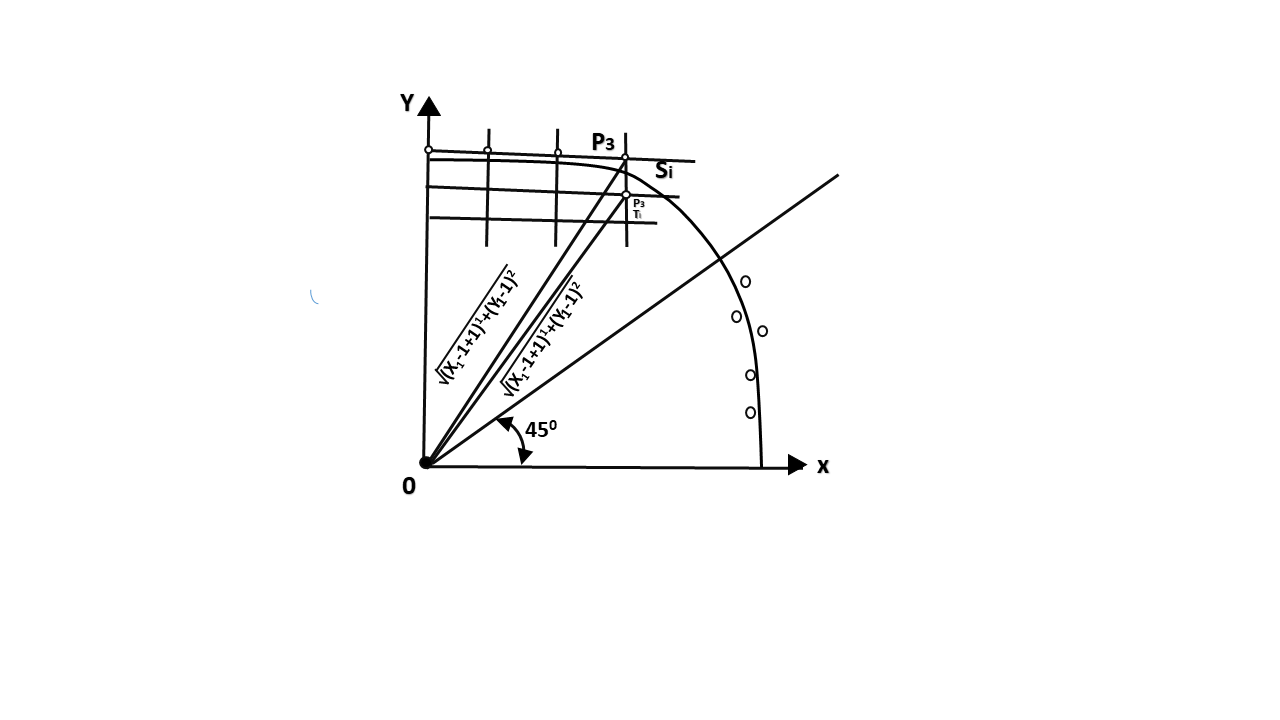
90° to 45°. Assume that the last scan-converted pixel is P1 as shown in fig. Each new point closest to the true circle can be found by taking either of two actions.
Let D (Si) is the distance from the origin to the true circle squared minus the distance to point P3 squared. D (Ti) is the distance from the origin to the true circle squared minus the distance to point P2 squared. Therefore, the following expressions arise.
D (Si)=(xi-1+1)2+ yi-12 -r2
D (Ti)=(xi-1+1)2+(yi-1 -1)2-r2
Since D (Si) will always be +ve & D (Ti) will always be -ve, a decision variable d may be defined as follows:
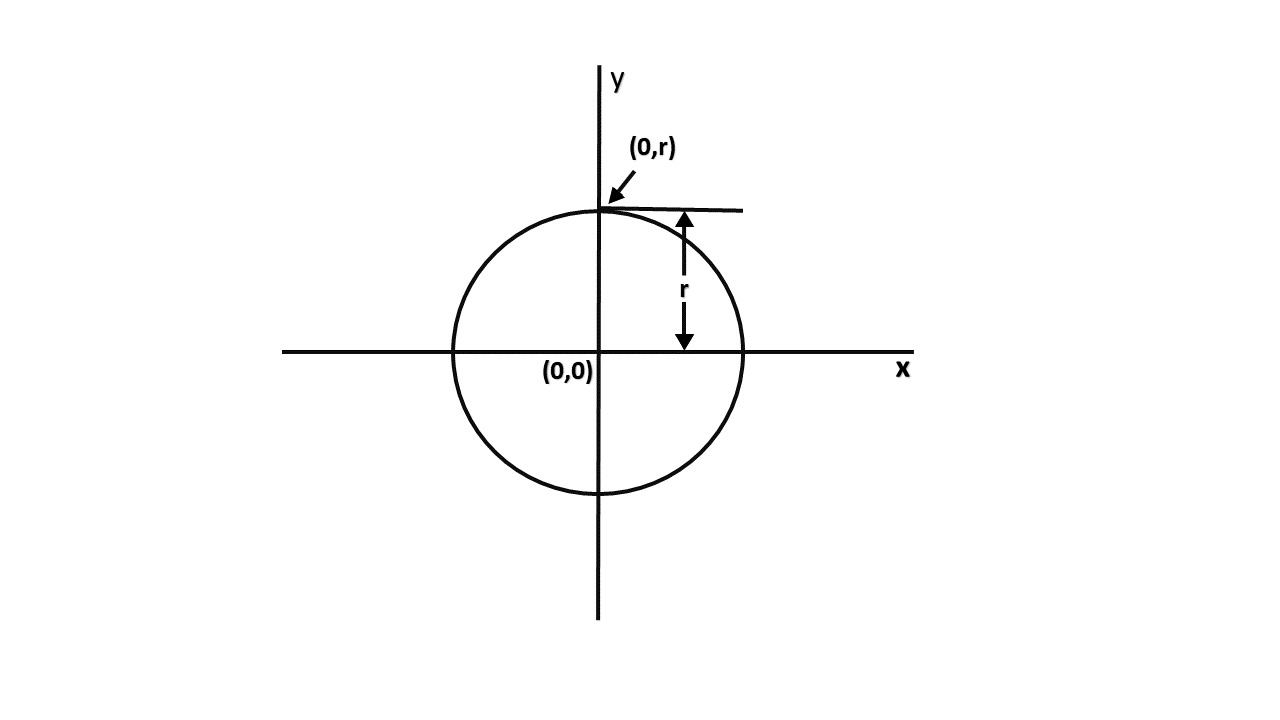
di=D (Si )+ D (Ti)
Therefore,
di=(xi-1+1)2+ yi-12 -r2+(xi-1+1)2+(yi-1 -1)2-r2
From this equation, we can drive initial values of di as
If it is assumed that the circle is centered at the origin, then at the first step x = 0 & y = r.
Therefore,
di=(0+1)2+r2 -r2+(0+1)2+(r-1)2-r2
=1+1+r2-2r+1-r2
= 3 - 2r
Thereafter, if d_i<0,then only x is incremented.
xi+1=xi+1 di+1=di+ 4xi+6
& if di≥0,then x & y are incremented
xi+1=xi+1 yi+1 =yi+ 1
di+1=di+ 4 (xi-yi)+10
Step1: Start Algorithm
Step2: Declare p, q, x, y, r, d variables
p, q are coordinates of the center of the circle
r is the radius of the circle
Step3: Enter the value of r
Step4: Calculate d = 3 - 2r
Step5: Initialize x=0
&nbsy= r
Step6: Check if the whole circle is scan converted
If x > = y
Stop
Step7: Plot eight points by using concepts of eight-way symmetry. The center is at (p, q). Current active pixel is (x, y).
putpixel (x+p, y+q)
putpixel (y+p, x+q)
putpixel (-y+p, x+q)
putpixel (-x+p, y+q)
putpixel (-x+p, -y+q)
putpixel (-y+p, -x+q)
putpixel (y+p, -x+q)
putpixel (x+p, -y-q)
Step8: Find location of next pixels to be scanned
If d < 0
then d = d + 4x + 6
increment x = x + 1
If d ≥ 0
then d = d + 4 (x - y) + 10
increment x = x + 1
decrement y = y - 1
Step9: Go to step 6
Step10: Stop Algorithm


What is ISO 9000 Certification? How to Get ISO 9000 Certification?

Why Required of ISO 9001:2000 standard?

Write a C program to find factorial(using recursion) of any no.

Write a C program to find minimum among three numbers.

Draw the ER diagram of a hospital and explain.


Write short note on Call setup of GSM network for mobile-to-mobile call.

Short Notes :Lines of Code (LOC)