State and prove maximum power transfer theorem
Statement:
The theorem states that a networks delivers maximum power to a resistive load connected across a voltage source when the load resistance is equal to the internal resistance of the voltage source as seen from the output terminals by removing the source and replacing the same by its internal resistance.
Proof:
The maximum power transfer theorem can be proved by considering a simple circuit consisting of a voltage source \(V_S\) in series with a source resistance \(R_S\) and a variable load resistance \(R_L\) connected at the output terminal as shown in Fig. 2. The current \(I_L\) flowing through the load resistance \(R_L\) is given by
\(I_L=\frac{V_S}{R_L+R_S}\)
The power delivered to the load is given by
\(P_L={I^2}_LR_L=\left(\frac{V_S}{R_L+R_S}\right)^2R_L\) … (1)
The power \(P_L\) depends of on the magnitude of \(R_L\) . Under both short circuited and open circuited conditions no power is delivered to the load , i.e., \(P_L=0\) when \(R_L=0\) or \(\infty\). The power delivered to the load becomes maximum for certain value of \(R_L\). This may be found out by equating \(\frac{dP_L}{dR_L}\) to zero as a condition for maximum power.
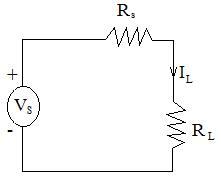Fig. 2 The circuit diagram for maximum power transfer theory
Differentiating equation (1) with respect to \(R_L\), we have
\(\frac{dP_L}{dR_L}={V^2}_S\left[\frac{\left(R_L+R_S\right)^2-{2R_L(R}_L+R_S)}{\left(R_L+R_S\right)^4}\right]\)
For the maximum value of power at the load, we have
\(\frac{dP_L}{dR_L}=0\)
\({V^2}_S\left[\frac{\left(R_L+R_S\right)^2-{2R_L(R}_L+R_S)}{\left(R_L+R_S\right)^4}\right]=0\)
\(\left(R_L+R_S\right)^2={2R_L(R}_L+R_S)\)
\({(R}_L+R_S)=2R_L\)
\(R_S=R_L\)
The maximum power across the load resistance \(R_L\), we have
\(\left(P_L\right)_{max}=\left(\frac{V_S}{R_L+R_L}\right)^2R_L=\frac{\left(V_S\right)^2}{4R_L}\)
The input power supply by the source is given by
\(\left(P_{in}\right)_{max}=V_SI_L=V_S\times\frac{V_S}{R_L+R_L}=\frac{\left(V_S\right)^2}{2R_L}\)
The efficiency \(\eta =\frac{{\left(P_{L}\right)}_{max}}{P_{in}} = \frac{1}{2}\) =50%
Determine the value R in Fig. 15(a) such that 4 Ω resistor consumes maximum power.
1.png)
Fig. 15(a)
What is meant by hysteresis in a magnetic circuit? What is the significance of B-H curve?
Write short notes on:
Write a short note on Bathe hole coupler.
Explain the tunneling action in a tunnel diode.
Write short notes on:
What is E-plane Tee? Derive its S-matrix.
