A 20 Ω resistor, a choke coil having some inductance and some resistance and a capacitor are connected in series across a 25 V variable frequency source. When frequency is 400 Hz, the current is maximum and its value is 0.5 Amp and the potential difference across the capacitor is 150 V. Calculate the resistance and the inductance of the chokes coil and the capacitance of the capacitor.
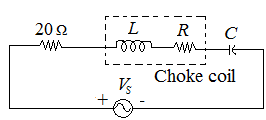
Fig. 16
The total impedance of the circuit is \(R_{eq}=20+R+j\omega L-\frac{1}{\omega C}\)
The maximum current is following through the circuit at the time of resonance. For the resonance \(X_L\) and \(X_C\) is same.
Therefore \(\omega L=\frac{1}{\omega C}\),
At the resonance the total current passing through the circuit \(I=\frac{V}{20+R}\)
Or \(0.5=\frac{25}{20+R}\) , \(R=30\ \mathrm{\Omega}\)
The voltage drop across the capacitor \(V_C=I\times X_C=I/\omega C\)
Or \(C=\frac{0.5}{150\times2\times\pi\times400}=1.33\ \mu F\)
\(\omega^2=LC\)
\(L=\frac{\omega^2}{C}=\frac{1\times1.33}{\left(2\pi\times400\right)^2\times{10}^{-6}}=210\ mH\)
Find the current in each branch of the network using Kirchhoff’s law
Fig.23
For the circuit shown bellow, determine the current i1,i2,i3 using nodal analysis
Establish the equivalence between Thevenin’s and Norton’s theorems.
What is Carson’s rule? Explain it.
What is E-plane Tee? Derive its S-matrix.
Explain PIN diode and give its application.
1.png)
Fig. 15(a)