Once object description has been transmitted to the viewing reference frame, we choose the window extends in viewing coordinates and selects the viewport limits in normalized coordinates.
Object descriptions are then transferred to normalized device coordinates:
We do this thing using a transformation that maintains the same relative placement of an object in normalized space as they had in viewing coordinates.
If a coordinate position is at the center of the viewing window:
It will display at the center of the viewport.
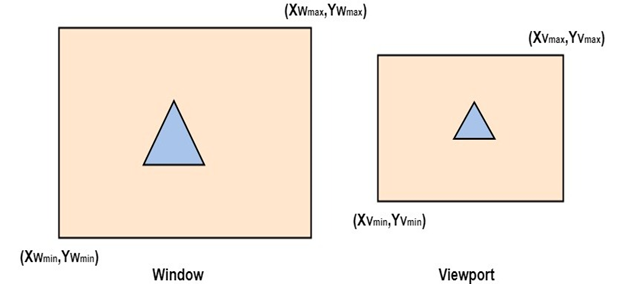
Fig shows the window to viewport mapping. A point at position (xw, yw) in window mapped into position (xv, yv) in the associated viewport.
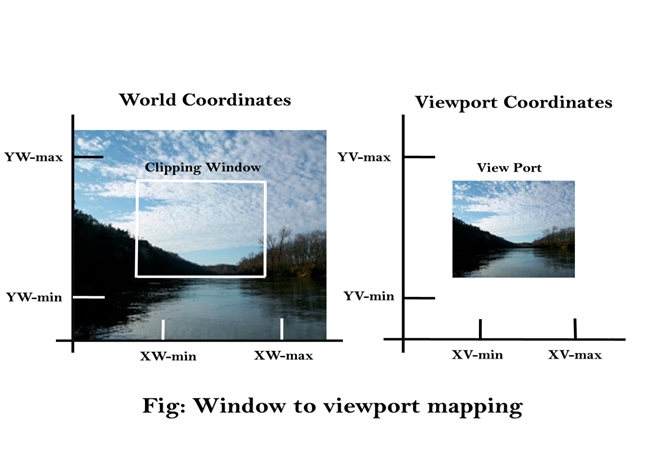
In order to maintain the same relative placement of the point in the viewport as in the window, we require:
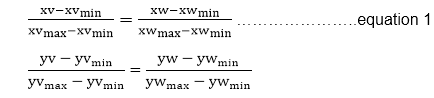
Solving these impressions for the viewport position (xv, yv), we have
xv=xvmin+(xw-xwmin)sx
yv=yvmin+(yw-ywmin)sy ...........equation 2
Where scaling factors are
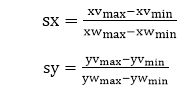
Equation (1) and Equation (2) can also be derived with a set of transformation that converts the window or world coordinate area into the viewport or screen coordinate area. This conversation is performed with the following sequence of transformations:
From normalized coordinates, object descriptions are mapped to the various display devices.
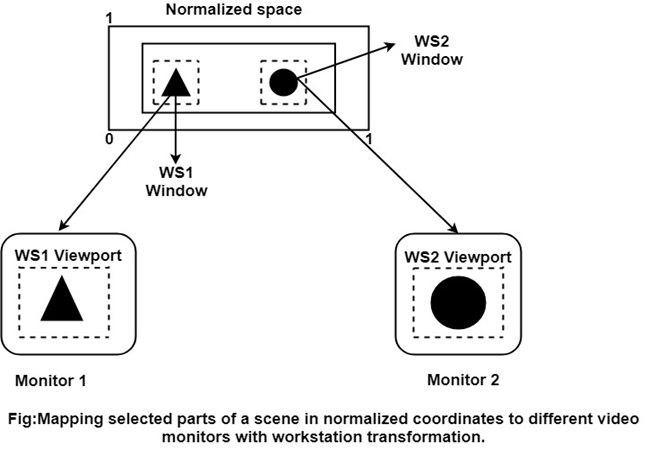
Any number of output devices can we open in a particular app, and three windows to viewport transformation can be performed for each open output device.
This mapping called workstation transformation (It is accomplished by selecting a window area in normalized space and a viewport area in the coordinates of the display device).
As in fig, workstation transformation to partition a view so that different parts of normalized space can be displayed on various output devices).
Step1:Translate window to origin 1
Tx=-Xwmin Ty=-Ywmin
Step2:Scaling of the window to match its size to the viewport
Sx=(Xymax-Xvmin)/(Xwmax-Xwmin)
Sy=(Yvmax-Yvmin)/(Ywmax-Ywmin)
Step3:Again translate viewport to its correct position on screen.
Tx=Xvmin
Ty=Yvmin
Above three steps can be represented in matrix form:
VT=T * S * T1
T = Translate window to the origin
S=Scaling of the window to viewport size
T1=Translating viewport on screen.
Viewing Transformation= T * S * T1
We can display picture at device or display system according to our need and choice.
Note:
What is Software Quality Management?
Create a Sparse Matrix in C.
Write an program to generate Pascal’s triangle.
Write the characteristics of a good user interface.
Write short notes on the following:
Write short note on
Iridium satellite system
Write a C program to find the multiplication table of any no.
