Describe the process of capacitance measurement using De Sauty’s bridge and draw the relevant phasor diagram. State the limitations of the bridge.
For measurement of capacitance and dissipation factor Schering bridge is widely used. The phasor diagram and circuit diagram of the bridge are as follows:
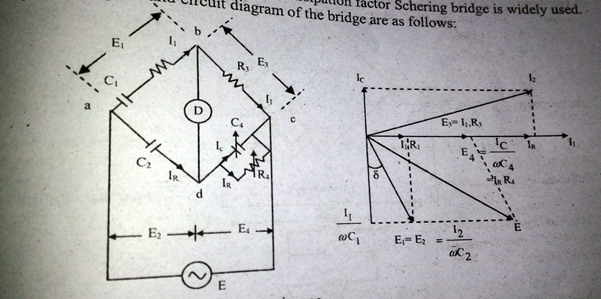
Let, \(C_1\) = Capacitor of unknown capacitance.
\(R_1\) = a series resistance representing the loss in capacitor \(C_1\).
\(C_2\) = a standard capacitor
\(R_3\) = a non-inductive resistance
\(C_4\) = a variable capacitor
\(R_4\) = a variable non-inductive resistance in parallel with \(C_4\).
At balance,
\(\left(r_1+\frac{1}{j\omega C_1}\right)\left(\frac{R_4}{1+j\omega C R_4}\right)=\frac{1}{j\omega C_2}.R_3\)
\(\left(r_1+\frac{1}{j\omega C_1}\right)R_4=\frac{R_3}{j\omega C_2}\left(1+j\omega C_4R_4\right)\)
\(r_1R_4-\frac{jR_4}{\omega C_1}=j\frac{R_3}{\omega C_2}+\frac{R_3R_4C_4}{C_2}\)
Equating imaginary and real parts,
\(r_1R_4=\frac{R_3R_4C_4}{C_2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore r_1=\frac{R_3C_4}{C_2}\)
and, \(-\frac{jR_4}{\omega C_1}=-j\frac{R_3}{\omega C_2}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \therefore\ C_1=\frac{R_4}{R_3}C_2\)
Dissipation factor \(D_1=tan\delta=\omega C_1r_1\)
What is the function of delay time?
Describe why modulation is necessary for communication.
Fig.23.png)
Fig.22(a)