Explain the relevant circuit diagram, the principle of measurement of low resistance by kelvin’s double bridge. Prove that the condition of balance is independent of the read resistance. Up to what low value it can be used?
The kelvin bridge is a notification of the Wheatstone bridge with greater increased accuracy in measurement of low value resistance.
Consider the bridge circuit shown in the figure.
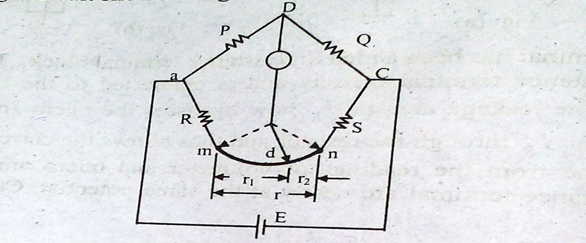
R= resistance of the lead that connects the unknown resistance R to standard resistance S.
Two galvanometer connections are indicated by dotted lines. The connection may be either to point ‘m’ or to point ‘n’.
As the galvanometer is connected to point m, the resistance r of the connecting leads is added to the standard resistance S resulting in indication of too low an indication for unknown resistance R. When the connection is made at the point n, the resistance is added to unknown resistance, which results in indication of much high a value for R. Assumed that instead of using point m, we give the low result for n, which makes the result high, we make the galvanometer to any intermediate point ‘d’ as soon by full line in fig. If a point ‘d’ the resistance r is divided into two parts \(r_1\) and \(r_2\) such that
\(\frac{r_1}{r_2}=\frac{P}{Q}\)
The presence of \(r_1\) the resistance of connectivity leads, causes no error in the result, we have
R+r_1=\ \frac{P}{Q}(\ s+r_2 ) \)
but, \(\frac{r_1}{r_2}=\frac{P}{Q}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots\left(1\right)\)
\(\frac{r_1}{r_1+r_2}=\frac{P}{P+Q}\)
\(r_1=\frac{P}{P+Q}\times r\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left[r_1+r_2=r\right]\)
r_2=\frac{Q}{P+Q}\times r\)
We can write equation (1) as
\(\left(R+\frac{P}{P+Q}.r\right)=\frac{P}{Q}\left(S+\frac{Q}{P+Q}.r\right)\)
\(R=\frac{P}{Q}.S\)
The kelvin double bridge involves the idea of a second set of ratio arms. Therefore, the name double bridge, the use of four terminal resistors for the low resistance arms. As from the figure, the first set of ratio arms is P and Q. The second set of ratio arms p and q is used to connect two galvanometers to a point d at the appropriate potential between points m and n to eliminate the effect of connecting lead of resistance r between the known resistance R and the standard resistance S.
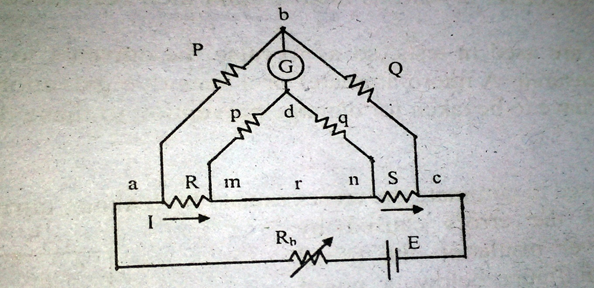
The ratio p/q is made equal to P/Q. Under balance conditions there is no current through the galvanometer,
\(E_{ab}\)=Voltage drop between a and b
\(E_{ac}\)=Voltage drop between a and c
\(E_{ab}=\frac{P}{P+Q}.E_{ac}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ E_{ac}=I\left[R+S+\frac{\left(p+q\right)r}{p+q+r}\right]\)
\(E_{amd}=I\left[R+\frac{P}{P+Q}\left\{\frac{\left(p+q\right)r}{p+q+r}\right\}\right]-I\left[R+\frac{pr}{p+q+r}\right]\)
For zero galvanometer deflection \(E_{ab}=E_{amd}\).
\(\frac{P}{P+Q}I\left[R+S+\frac{\left(p+q\right)r}{p+q+r}\right]=I\left[R+\frac{pr}{p+q+r}\right]\)
\(R=\frac{P}{Q}.S+\frac{qr}{p+q+r}\left[\frac{P}{Q}-\frac{p}{q}\right]\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots\left(2\right)\)
if \(\frac{P}{Q}=\frac{p}{q}\), Equation (2) becomes \(R=\frac{P}{Q}.S\)
How can potentiometer be used for
What are the special features of a high voltage Schering bridge? What is meant by “Wagner’s Earth”?
