Explain with suitable block diagram the generation of FM signal using Armstrong method.
The generation of FM waveform by indirect method is also known as Armstrong Method. In the indirect method a narrow band FM signal is generated first after that this NBFM signal is frequency multiplied to generate WBFM. The simple block diagram for generation WBFM signal by indirect method is shown in Fig.6
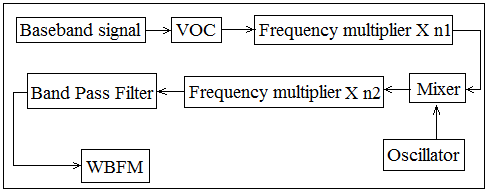
Fig. 6 WBFM generation process
The NBFM signal is generated by the baseband signal x(t) with the VCO. The NBFM signal is then converted into WBFM using frequency multipliers. The frequency component of the WBFM goes to higher value by the process of frequency multiplication. After 1st time frequency multiplication the output signal farther modulated with carrier signal by the mixer which is generated by the local oscillator. The output signal of the mixer again multiplied with the higher frequency and the modulated signal goes to higher order frequency signal. Finally the high frequency signal is passed through the band pass filter to obtain desire signal.
The modulated signal at the output of VCO is
\(S_1\left(t\right)=A_1cos\left(2\pi f_1t++2\pi k_1\int_{0}^{t}x\left(t\right)dt\right)\)
Where f1is the frequency of the carrier inside the VCO and k1 is the constant
The output signal of frequency multiplier block 1 is
\(S_2\left(t\right)=A_2cos\left(2\pi n f_1t+2\pi n k_1\int_{0}^{t}x\left(t\right)dt\right)\)
Here nf1 = f2 and nk1 = k2
\(S_2\left(t\right)=A_2cos\left(2\pi f_2t+2\pi k_2\int_{0}^{t}x\left(t\right)dt\right)\)
After 2nd time frequency multiplication we have the WBFM signal.
Here mf2 = fc and mk2 = kf
\(S_2\left(t\right)=A_2cos\left(2\pi{mf}_2t+2\pi{mk}_2\int_{0}^{t}x\left(t\right)dt\right)\)
\(S\left(t\right)=A_ccos\left(2\pi f_ct+2\pi k_f\int_{0}^{t}x\left(t\right)dt\right)\)
This above signal is passed through the BPF and desired signal is obtained.
Explain the tunneling action in a tunnel diode.
State and prove maximum power transfer theorem
State and prove the Parseval’s theorem for power.
