A carrier signal \(A_ccos\omega_ct\) is amplitude modulated by a message signal \(A_mcos\omega_mt\), where \(A_m<A_c\)
\(s\left(t\right)=\left(A_c+A_mcos\omega_mt\right)cos2\pi f_ct\) ………….….. (1)
Where \(m_a=\frac{\left|A_m\right|}{A_c}\) for all \(A_c\geq A_m\) and it is called modulation index.
\(A_m\) and \(A_c\) are the amplitude of the message and carrier signal.
The percentage of modulation is equal to \(\frac{\left|A_m\right|}{A_c}x100\)
\(s\left(t\right)=A_c\left[1+m_acos\omega_mt\right]cos2\pi f_ct\) …………….. (2)
\(cos2\pi f_ct=\frac{e^{-j2\pi f_ct}+e^{j2\pi f_ct}}{2} , s\left\{\left(t\right)\right\}=S\left(f\right) and cos2\pi f_mt=\frac{e^{-j2\pi f_mt}+e^{j2\pi f_mt}}{2}\)
After taking Fourier transform, we have
\(S\left(f\right)=\frac{A_c}{2}\delta\left(f+f_c\right)+\frac{A_c}{2}\delta\left(f-f_c\right)+\frac{A_cm_a}{4}\delta{\left\{f+\left(f_c+f_m\right)\right\}}+\frac{A_cm_a}{4}\delta{\left\{f-\left(f_c+f_m\right)\right\}}\)$$+\frac{A_cm_a}{4}\delta{\left\{f+\left(f_c-f_m\right)\right\}}+\frac{A_cm_a}{4}\delta{\left\{f-\left(f_c-f_m\right)\right\}}$$ ……….. (3)
The single tone sinusoidal amplitude modulation in frequency domain is representd by equation (3). The 1st, 2nd terms of equation (3) are the carrier component and remaining four components are the expression of single tone message signal.
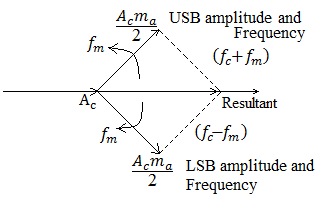
Fig. 16 Phasor diagram of single tone sinusoidal AM signal.
.png)
Fig. 20(a)