A coil of resistance 30 Ω and inductance 320 mH is connected in parallel to a consisting of 75 Ω in series with 150 µF capacitor. The circuit is connected to a 200 volt, 50 Hz supply. Determine supply current and circuit power factor.
The circuit diagram with resistance, inductance and capacitance are given in Fig. 9.
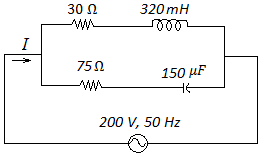Fig. 9 circuit diagram according to the problem 7(b)
Inductive reactance \(X_L=j\omega L=j\times2\pi\times f\times L=j\times2\times\frac{22}{7}\times50\times320\times{10}^{-3}\)
\(X_L=100.48\ \mathrm{\Omega}\)
Capacitive reactance \(X_C=\frac{1}{j\omega C}=\frac{1}{j\times2\times\pi\times f\times C}=\frac{1}{j\times2\times\frac{22}{7}\times50\times150\times{10}^{-6}}=21.23\ \mathrm{\Omega}\)
The conductance of coil for the resistance \(R_1=30\ \mathrm{\Omega}\) and inductive reactance \(X_L=100.48\ \mathrm{\Omega}\) is
\(G_1=\frac{R_1}{\left(R_1\right)^2+\left(X_L\right)^2}=\frac{30}{\left(30\right)^2+\left(100.48\right)^2}=2.73\ ℧\)
The susceptance of the coil is
\(B_1=-\frac{X_L}{\left(R_1\right)^2+\left(X_L\right)^2}=-\frac{100.48}{\left(30\right)^2+\left(100.48\right)^2}=-9.14\times{10}^{-3}\ ℧\)
The conductance of the capacitor for the resistance \(R_2=75\ \mathrm{\Omega}\) and capacitive reactance \(X_C=21.23\ \mathrm{\Omega}\) is
\(G_2=\frac{R_2}{\left(R_2\right)^2+\left(X_C\right)^2}=\frac{75}{\left(75\right)^2+\left(21.23\right)^2}=12\times{10}^{-3}\ ℧\)
The susceptance of the coil is
\(B_2=\frac{X_C}{\left(R_2\right)^2+\left(X_C\right)^2}=-\frac{21.23}{\left(75\right)^2+\left(21.23\right)^2}=-3.49\times{10}^{-3}\ ℧\)
The total conductance of the given circuit is \(G=G_1+G_2=(2.73+12)\times{10}^{-3}=14.73\times{10}^{-3}\ ℧\) and total susceptance is \(B=B_1+B_1=(-9.14+3.49)\times{10}^{-3}=-5.65\times{10}^{-3}\ ℧ \)
Total admittance of the circuit \(Y=\sqrt{\left(G\right)^2+\left(B\right)^2}=\sqrt{\left(14.73\right)^2+\left(5.65\right)^2}\times{10}^{-3}=0.016\ ℧ \)
Supply current through the circuit \(I=V\times Y=200\times0.016=3.2\ Amp\).
The power factor of a circuit is \(F=\cos{\mathrm{\Phi}}=\frac{G}{Y}=\frac{14.73\times{10}^{-3}}{0.016}=0.92\)
Find the current in each branch of the network using Kirchhoff’s law
Fig.23
Draw a mathematical expression for RMS value of a sinusoidal voltage \(v=V_{m}\sin{{\omega t}}\).
Write short note on PCM ( Pulse Code Modulation).
Compare AM and NBFM.
What is meant by entropy of a source?
Find the Fourier transform of the following:
Fig. 1
.png)
Fig. 18(a)