Write short notes on
Cavity Resonator:
At low frequency, the frequency of oscillation of an L-c circuit is given by
\(f=\frac{1}{2\pi\sqrt{LC}}\)
But at microwave frequency, the value of L and C will be so small that they cannot be practically realizable. At microwave the cavity resonator the cavity resonator can generate oscillation like L.C tuned circuit. When a short is placed across the waveguide, the wave reflected by the short, forms a standing wave along with the incident wave. At the position of the short, there is a voltage minimum and these minima are repeated at half wave length intervals from the short. Now another short is placed at one of the voltage minima, then there will be completed reflection back towards the 1st short at which is now in phase with the original signal. Thus the cavity from by the waveguide and the two shorting plates can support signal having form by the waveguide and the two shorting plates can support signal having a back and forth motion and produced oscillations. This continues until all the applied energy is dissipated. If cavity resonator as an infinite number of resonant frequencies. Since, standing wave can also exist in co-axial waveguide, hence co – axial resonator is also possible. In practice the cavity resonator may be rectangular cavity, circular cavity, and reentrant cavity types.
Rectangular cavity resonator:
The rectangular cavity resonator is shown in Fig. 36. Waveguide cavity resonators are formed by shorting two ends of a section of a waveguide and the reflected waves of the shorting plates forms the standing wave. If the distance between the two shorting plates is multiple of \(\frac{\lambda_g}{2}\) , then the signal moves back and forth between the two plates and produces resonance. The cavity resonator can resonant at only one particular frequency like a parallel resonant circuit.
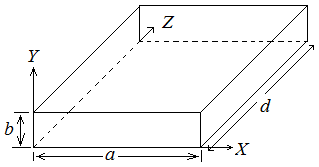
Fig. 36 Rectangular cavity resonator
Here the electric field is zero at z=0 and z=d, because of the short and also the tangential electric field E is zero at four walls, is the another boundary condition.
The resonance frequency of rectangular cavity resonator is same for both Te and TM modes.
For TE101 mode m=1, n=0, p=1
Therefore the resonance frequency
\(f_r=\frac{1}{2d\sqrt{\mu\epsilon}}\sqrt{1+\left(\frac{d}{a}\right)^2}\)
Hybrid Ring:
The hybrid ring or rat race couple is given in Fig. 37. It is another type of four port hybrid junction knows as rat race coupler or hybrid ring. Each port is separated from its next port by a distance of \(\frac{\lambda_g}{4}\) and hence incident power at port 1 is dividing equally in two directions and when reaches to port 4 travels equal distance \(\frac{3\lambda_g}{4}\) in both clockwise and in anticlockwise directions and hence phase addition takes place at port 4.
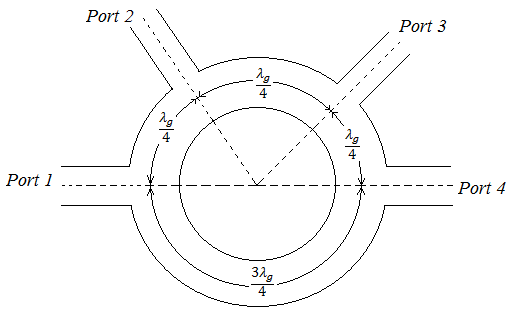
Fig. 37 Rat race coupler (Hybrid ring)
Similarly, at port 2, the portion of signal travelling clockwise travels \(\frac{\lambda_g}{4}\) and that travelling counter – clockwise covers \(\frac{{5\lambda}_g}{4}\) and the two portions are again in phase resulting in addition at port 2 and results propagation through port 2. As far as port 3 is concerned, the input signal of port 1 travels distance of \(\frac{\lambda_g}{2}\) in clockwise direction and travels a distance of \(\lambda_g\) in the anticlockwise direction, hence the two components reacting port 3 are out of phase and they cancel each other, resulting in no power output from port 3.
Similarly, it can be shown that port 3 is transferring power to port 2 and port 4 but isolated from port 1 and the behavior is similar to that of magic Tee.
Compare PAM, PWM and PPM
Establish the equivalence between Thevenin’s and Norton’s theorems.
