What is bunching? Explain with proper diagram. Deduce the expression for the minimum length at which the first bunch will be formed.
Electrons in the electron beam produced in the cathode – anode region of the Klystron and accelerated by a d.c anode voltage passing through a pair of buncher grids, across which an R.F voltage exist are either accelerated or decelerated depending on the part of the cycle during which they cross the gap. The accelerated electrons emerge with higher velocity than the entering velocity and those with decelerated energy with velocity lower than the entering velocity. Some electrons pass through at zero fields and hence suffer no change in velocity. This variation of velocities of the electrons in the electron beam is known as velocity modulation.
When the velocity modulated electrons drift in the region they are converted into density modulation, a process commonly known as bunching in Klystron.
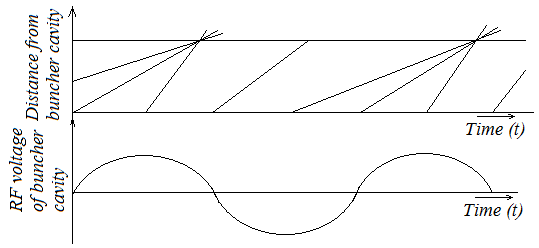Fig. 7 Bunching in Klystron Amplifier
Fig. 8 shows the bunching distance, i.e. the trajectories of minimum, zero used and maximum electron acceleration. The distance from the buncher grid to the location of dense electron bunching for the electron at TB is
∆L=v0(TD-TB) … (i)
Similarly, the distance for the electrons at TA and TC are
\(∆L=V_{min}\left(T_D-T_A\right)=V_{min}\left(T_D-T_B+\frac{\pi}{2\omega}\right)\) … (ii)
\(∆L=V_{max}\left(T_D-T_C\right)=V_{max}\left(T_D-T_B-\frac{\pi}{2\omega}\right)\) … (iii)
Now the expressions for minimum and maximum velocities are
\(V_{min}=V_0(1-\frac{V_1\beta_i}{2V_0})\) … (iv)
\(V_{min}=V_0(1+\frac{V_1\beta_i}{2V_0})\) … (v)
When βi=beam-coupling coefficient, V1=signal amplitude
V0=d.c voltage,v0=electron velocity
After substitution, we have
\(∆L=V_0\left(T_D-T_B\right)+\left[v_0\frac{\pi}{2\omega}-v_0\frac{V_1\beta_i}{2V_0}\left(T_D-T_B\right)-v_0\frac{V_1\beta_i}{2V_0}\frac{\pi}{2\omega}\right]\) … (vi)
\(∆L=V_0\left(T_D-T_B\right)+\left[-v_0\frac{\pi}{2\omega}-v_0\frac{V_1\beta_i}{2V_0}\left(T_D-T_B\right)+v_0\frac{V_1\beta_i}{2V_0}\frac{\pi}{2\omega}\right]\) … (vii)
The necessary condition for those electrons at TA, TB and TC to meet at the same distance ∆L is
\(v_0\frac{\pi}{2\omega}-v_0\frac{V_1\beta_i}{2V_0}\left(T_D-T_B\right)-v_0\frac{V_1\beta_i}{2V_0}\frac{\pi}{2\omega}=0\) … (viii)
and \(-v_0\frac{\pi}{2\omega}-v_0\frac{V_1\beta_i}{2V_0}\left(T_D-T_B\right)+v_0\frac{V_1\beta_i}{2V_0}\frac{\pi}{2\omega}=0\) … (ix)
consequently, \(T_D-T_B=\frac{\pi V_0}{\omega V_1\beta_i}\)
and ∆L=v0(πV0/ωV1βi)
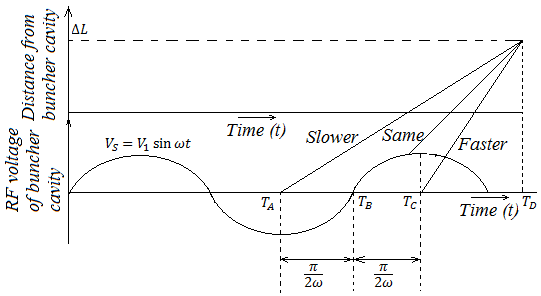Fig. 8 Bunching distance
What is Gunn diode oscillator? What are different modes of operation of Gunn diode? Mention its applications.
Derive the expression for overall noise figure of a cascaded system.
Write a short note on TDM (Time Division Multiplexing).
What is Carson’s rule? Explain it.
Write short notes on:
