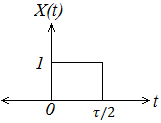From the figure, we have the function x(t) = 1 for 0 < t ≤ τ/2 and otherwise x(t) = 0

The general expression of Fourier transform is

$$  X(f) = \int_{-\infty}^{\infty} x(t) e^{-i 2 \pi f t} \, dt $$

$$ \begin{align*}
X(f) &= \int_{0}^{\tau/2} e^{-j 2 \pi f t} \, dt \\
     &= \frac{1}{-j 2 \pi f} \left[ e^{-j 2 \pi f t} \right]_{0}^{\tau/2} \\
     &= \frac{-1}{j 2 \pi f} \left[ e^{-j \pi f \tau / 2} - 1 \right] \\
     &= \frac{-1}{j 2 \pi f} \left[ e^{-j \pi f \tau / 2} \times e^{-j \pi f \tau / 2} - e^{-j \pi f \tau / 2} \times e^{j \pi f \tau / 2} \right]
\end{align*} $$

$$ X(f) = \frac{1}{j 2 \pi f} e^{-j \pi f \tau / 2} \left[ \frac{e^{-j \pi f \tau / 2} - e^{j \pi f \tau / 2}}{2} \right] $$

$$ X(f) = \frac{e^{-j \pi f \tau / 2} \sin\left(\frac{j \pi f \tau}{2}\right)}{\pi f} $$