How is a Phase Locked Loop (PLL) used for demodulation of FM signal? Mention the advantage of PLL demodulation.
The PLL is useful in demodulation of FM signals in presence of large noise and low signal power (low signal to noise ratio). It is most switched for using space vehicle to earth data links or where loss along the transmission path is very large recently it has found application is commercial FM receivers.
A PLL is basically a negative feedback system shown in the Fig.4 below.
This consists of three major’s components a multiplier, a loop filter and a voltage control oscillator (VCO) connected together in a form of feedback loop.
Fig.4 Basic Block diagram of PLL.
The operation of PLL is similar to any other feedback system. In a typical feedback system, the feedback signal tense to follow the input signal. If the signal feedback is not equal to the input signal, the difference signal (known as the error signal) will change the value of the feedback signal until it is equal to the input signal. A PLL operate on a similar principal except for the fact that the quantity feedback is not the amplitude, but a generalized phase ∅(t). The error signal is utilized to adjust the VCO frequency in such a way that the instantaneous phase angle comes close to the angle of the incoming signal. At this point, the two signals, that is incoming and VCO output signals are in synchronism and the PLL is locked to the incoming signal
\(\frac{d\emptyset_1\left(t\right)}{dt}=\frac{d\emptyset_e\left(t\right)}{dt}+2\pi k_0\int_{0}^{t}{\emptyset_e\left(t\right)h\left(t-\tau\right)d\tau}\) ... (1)
Now taking Fourier transform of equation (1), we have
\(\phi_e\left(f\right)=\frac{1}{1+k_0\frac{H\left(f\right)}{jf}}\phi_1\left(f\right)\) ... (2)
After simplification of the PLL circuit, we have the expression given below
\(v\left(t\right)=\left(\frac{k_f}{k_v}\right)x\left(t\right)\) ... (3)
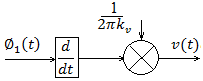
Fig.5 Simplified model of PLL for FM detection.
Therefore the output v(t) of phase locked loop is approximately same, except for a scale factor \(\left(\frac{k_f}{k_v}\right) \), as the original base band signal x(t).
So, the demodulated signal is proportional to the baseband signal.
Advantageous applications of PLL:
As a Tracking Band-Pass Filter for Angle Modulated Signals
In CW Carrier Recovery
As a frequency divider and multiplier
As a amplifier for angle modulated signals
For frequency synthesis and angle modulation
For coherent demodulation
In PM Demodulator
In FM Demodulator
In AM Demodulator
As a Suppressed Carrier Recovery Circuits
As a Squaring Loop
As a Costas Loop
Inverse Modulator
As a Clock Recovery Circuit
Write short notes on:
Write short notes on:
Describe why modulation is necessary for communication.
State and explain Biot – Savart law.
What is meant by entropy of a source?
Establish the equivalence between Thevenin’s and Norton’s theorems.
