What do you mean by thermal and white noise?
Thermal noise (Johnson noise):
The thermal noise also known as Johnson noise. The free electrons within a conductor are always in random motion. This random motion is due to the thermal energy received by them. The distribution of this free electrons within a conductor at a given instant of time is not uniform. It is possible that an excess number of electrons may appear at one end and the other of the conductor. The average voltage resulting from this non uniform distribution is zero but the average power is not zero. At this power results from the thermal energy, it is called as the thermal noise power.
The average thermal noise power is given by
\(P_n=kTBwatts\)
Where, \(k=Boltzmann^\prime sconstant=1.38\times{10}^{-23}\frac{Joules}{Kelvin}\)
T=Temperature of the conductor ∈ Kelvin
B=Bandwidth of the noise spectrum
The thermal noise power is directly proportional to the temperature of the conductor and bandwidth of the noise spectrum.
White noise:
The noise analysis in communication system is best on an idealized form of noise process called white noise. The white noise contain different ranges all the frequencies component in equal ratio and it is compared with white light where the spectrum of different wavelength are present. In this connection such type of noise is called white noise. The power spectral noise density (psd) of this noise is considered to be independent of frequency.
The power spectral density (psd) of white noise is represented by \(S_w\left(f\right)=\frac{N_0}{2}\) ...(6.1)
Where (1/2) indicate that half of the power is associated with the frequency and remaining half with negative frequencies. The quantity number has a dimension of w/Hz. The psd of white noise indicate that it has no dc power, and mean or average value of white noise process is zero.
The autocorrelation function of the psd can be obtain by taking the inverse Fourier Transform on both sides of equation (1). The autocorrelation function is defined as
\(R_w\left(\tau\right)=\frac{N_0}{2}\delta\left(\tau\right)\) ... (6.2)
Thus the autocorrelation function of the white noise consists of a delta function scaled by factor \(\frac{N_0}{2}\) and occurring \(\tau=0\). So \(R_w\left(\tau\right)=0\) for \(\tau\neq0\).
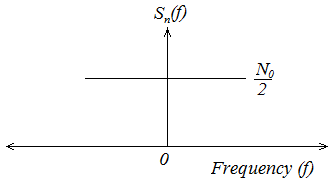Fig. 26 Spectrum of white noise
In strict sense white noise has infinite average power and is therefore physically realizable. Wherever, white noise has convenient mathematical properties and therefore is useful for system analysis. The role of white noise process in noise analysis is similar to the one played by an impulse function of delta function in the linear system analysis. Like impulse function, the effect of white noise observed only after passing it through a system with finite bandwidth.
Write short notes on:
Write short note on PCM ( Pulse Code Modulation).
State Ampere’s Circular law.
Describe why modulation is necessary for communication.
