For measurement of capacitance and dissipation factor Schering bridge is widely used. The phasor diagram and circuit diagram of the bridge are as follows:

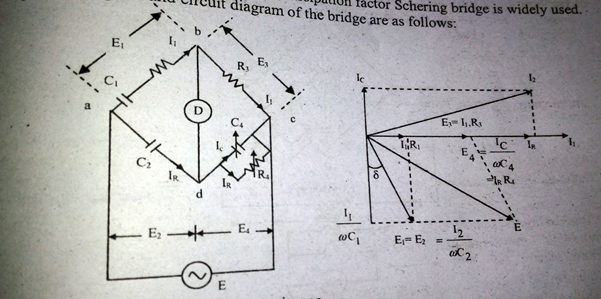
Let, $C_1$ = Capacitor of unknown capacitance.

$R_1$ = a series resistance representing the loss in capacitor $C_1$.

$C_2$ = a standard capacitor

$R_3$ = a non-inductive resistance

$C_4$ = a variable capacitor

$R_4$ = a variable non-inductive resistance in parallel with $C_4$.

At balance,

$(r_1+\frac{1}{j\omega C_1})\left(\frac{R_4}{1+j\omega C{R}_4}\right)=\frac{1}{j\omega C_2}.R_3$

$(r_1+\frac{1}{j\omega C_1})R_4=\frac{R_3}{j\omega C_2}(1+j\omega C_4{R}_4)$

$r_1{R}_4-\frac{j{R}_4}{\omega C_1}=j\frac{R_3}{\omega C_2}+\frac{R_3{R}_4{C}_4}{C_2}$

Equating imaginary and real parts,

$r_1{R}_4=\frac{R_3{R}_4{C}_4}{C_2}\therefore r_1=\frac{R_3{C}_4}{C_2}$

and, $-\frac{j{R}_4}{\omega C_1}=-j\frac{R_3}{\omega C_2}\therefore C_1=\frac{R_4}{R_3}{C}_2$

Dissipation factor $D_1=tan\delta =\omega C_1{r}_1$